Light Measurements Explained
What are lumens? How to measure light? How many watts a LED bulb consumes? These are just few of the topics about light covered in this article. We have tried to explain the fundamentals of light and how different aspects of light are measured using real life examples, highlighting the most important formulas, using informational images, graphics and tables, and also have made few calculators for easier calculations. Hope you find this article useful and if you have any comments, suggestions or additions, feel free to use the comment form below the article.
Here is a table of contents with links to topics covered in this article for easier navigation:
- LUMENS AND CANDELAS (luminous flux, light intensity)
- ILLUMINANCE, LUMINANCE, LUX AND FOOT-CANDLES
- HOW TO MEASURE LIGHT?
- LUMENS AND WATTAGE
LUMENS AND CANDELAS
What is a lumen?
Luminous flux or luminous power measures the total amount of light emitted by a light source over a period of time. In simple words, luminous flux tells how much light a lamp puts out in all directions per second, luminous flux is expressed in units called lumens (lm). Luminous flux only measures light radiated over visible wavelengths to a human eye from about 400-750 nm.
Lumen definition – lumen (lm) is a measurement unit of a luminous flux or luminous power. One lumen equals the amount of light emitted by a light source (radiating equal amount of light in all directions) through a solid angle of one steradian with an intensity of 1 candela.
Luminous flux (in lumens) is usually indicated on the packaging of a light bulb (or can be found in special catalogs of light bulbs) and is used as an objective measurement of the light output of a light source to better compare various types of light bulbs. However, because lumens are measured at a specific distance in all directions from the light source, it isn’t the best measurement to describe how bright a light is going to be on a specific area. To describe this, a term called Illuminance and units called lux or foot-candle are used.
Light intensity (candela)
Luminous intensity is the luminous power or the quantity of visible light emitted by a light source in a given direction per unit solid angle. Luminous intensity is measured in candela (cd) which is a SI base unit. Basically, it measures the quantity of visible light emitted in one specific angle from the light source, which is a useful measurement when comparing devices that produce focused beam of light such as spot lights, flashlights and laser pointers.
Candela definition – candela (cd) is a measurement unit in SI of luminous intensity. Candela replaced the older unit that was used to express luminous intensity – candlepower. One regular candle emits approximately 1 candela of luminous intensity, this is why candela was also called candle in older times.
Because candle was not the most precise light source to measure light intensity, a lot stricter rules and definition for measuring light intensity were defined, the official definition of candela:
The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 x 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian.
From http://physics.nist.gov/cuu/Units/current.html
Explanation
To recap, luminous flux measures how much total visible light is emitted by a light source, the unit of luminous flux is lumen (lm). Luminous intensity measures how much light is emitted by a light source in a single direction, the unit of luminous intensity is candela (cd). So basically, if you need a light bulb that emits light in all directions (for example ceiling light in a house) look at lumens when comparing various bulbs, however, if you need a light that can focus the maximum amount of brightness in a smaller beam such as a spot light or a flashlight, look at candelas when comparing such lights. Besides these two, illuminance is also an important metric, measuring the amount of light falling on a given surface (measured in lux or foot-candles), but later with this.
The classical example of explaining lumens and candelas: Imagine that you place a transparent sphere with 1 meter radius over a candle. The candle produces light intensity of 1 candela and emits light uniformly in all directions. If you cut a 1 square meter large hole in the sphere, 1 lumen of light would come out of that hole. This gives as an equation:
1lm = 1cd * sr
where:
- 1 lm = one lumen;
- 1 cd = one candela;
- sr = steradian (square radian, one square radian of a general sphere can be calculated using an equation A = r², where r is radius of a sphere).
So in this case:
1 lumen = 1 candela; a light source with 1 candela intensity produces 1 lumen of luminous flux in a sphere with 1 square meter surface area.
We can also calculate the luminous flux of entire sphere using the same equation. To do this, first we need to know the surface area of the sphere, this can be calculated using a formula:
4π r² = 4*3,14*1=12,56sr
So if we take the previous equation 1lm = 1cd * sr, and know that the light intensity is 1cd and the surface area of the sphere is 12,57m², we can calculate:
lm= 12,57; a light source with 1 candela intensity produces 12,57 lumens of luminous flux in a sphere with 1 meter radius (or 12,57m² surface area).
The same equation can be transformed to calculate candelas:
1cd = 1lm / sr
Lets look at a new example, we have a light bulb that emits 700 lumens of light uniformly in all directions, with the same transparent sphere with 1m radius over the bulb.
Now if we take the transformed formula 1cd = 1 lm / sr and know that the light flux equals 700lm and sphere surface area equals 12,57m², we can calculate the light intensity of the bulb:
700lm/12,57sr ≈ 56 cd
But if we want to calculate the light intensity in a certain direction, lets say passing through one steradian as in the first example, we can use the same formula:
To even better illustrate the difference between luminous flux (lumens) and luminous intensity (candelas), imagine a light bulb that produces 1 candela or 12,57 lumens, if you cover one side of the bulb it will still produce the same light intensity of 1 candela, but half the luminous flux – 6,28lm. This is because candelas measure the power of light, how bright the light will be in a certain direction, so in this case covering half of the bulb won’t affect the intensity of the light (if it’s measured at uncovered part of the bulb). But because lumens measure the total amount of visible light from the source, covering half of the bulb will decrease the total amount of visible light by half.
This is why you should compare candelas when purchasing a spot light or flashlight with concentrated light beam and lumens (or lux) when purchasing indoor lighting such as ceiling lights or outdoor flood lighting.
These previous calculations and formulas were mostly attributable to a light source that is isotropic or in other words, emits light uniformly to all directions. Now lets look how to calculate candelas and lumens in light bulbs at certain angles.
Lumens, candelas, viewing angles
In the same 1cd = 1lm / sr equation, sr indicates the viewing angle (also called apex angle) through which a light is emitted when calculating luminous intensity and luminous flux. In previous examples we calculated lumens and candles assuming that light is emitted uniformly to all directions (or in one example through a solid angle of one steradian, where 1 lumen equaled 1 candela), but usually we purchase lighting fixtures that illuminates light in a certain angle, spot lights illuminate in a narrower angle to provide more focused beam while flood lights illuminate in a wider angle to cover larger surface area.
When looking at the same equation 1cd = 1lm / sr, we can conclude that by increasing the luminous intensity (candelas), we should decrease the viewing angle (steradians) to produce the same luminous flux (lumens).
And in opposite, if we decrease the luminous intensity (candelas), we should increase the viewing angle (steradians) to produce the same luminous flux (lumens). So we can say that luminous intensity is inversely proportional to the viewing angle, meaning that increasing one value at the same rate, the other will decrease.
At the same time when calculating luminous flux, if we increase either the luminous intensity or the viewing angle, the luminous flux will increase, and in opposite, if we decrease either the luminous intensity or the viewing angle, the luminous flux will also decrease.
So how can we determine this apex angle of a light beam?
Basically, the apex angle is the angle between the axis of a light source that gives out the highest luminous intensity and the axis where the luminous intensity decreases to 50%. The formula to calculate the solid angle (Ω) in steradians (sr):
Ω = 2π(1−cos(α/2))
where α is the apex angle measured in degrees.
So, for example, if want to calculate the solid angle (Ω) in steradians (sr) to calculate lumens or candela of a light course, lets say for a light beam with an apex angle of 40°, using the above equation we get:
Ω ≈ 2*3,14*(1-0,94)
Ω ≈ 6,28*0,06
Ω ≈ 0,38sr
Now if we want to calculate the luminous flux of a light source with 1 candela intensity and viewing angle of 40°, we can insert the previously calculated solid angle Ω ≈ 0,38sr in the basic equation:
lm = 1*0,38
lm ≈ 0,38
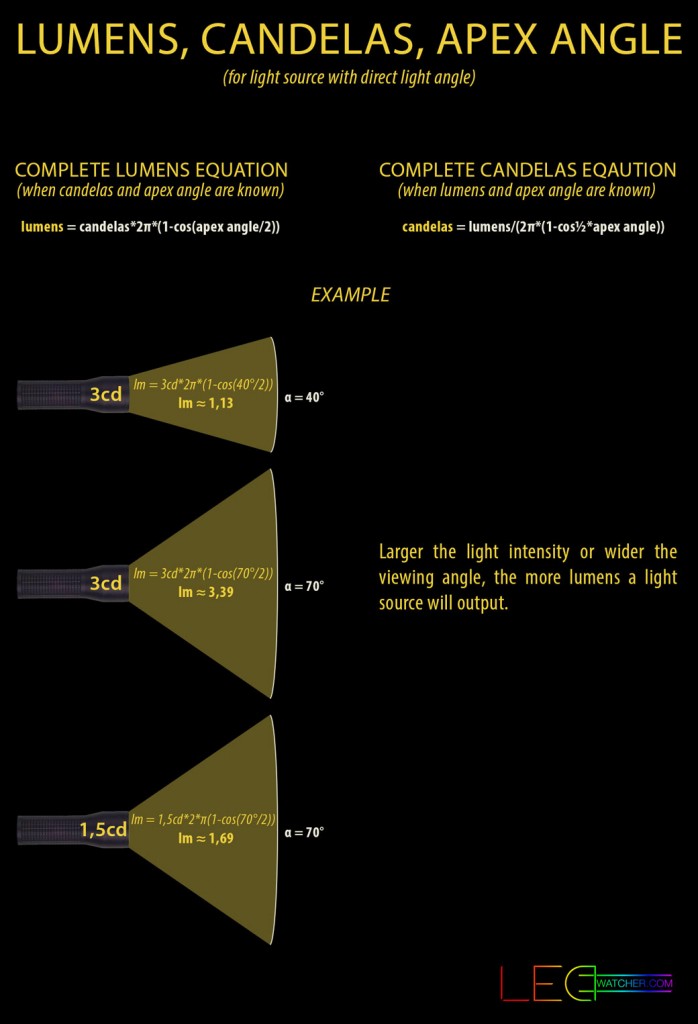
The full equation to calculate luminous flux (lumens) of a light source, if we know luminous intensity (candelas) and apex angle (steradians) is:
Φ=I2π(1−cos(α/2))
lumens = candelas*2π*(1-cos(apex angle/2))
- Φ – luminous flux (lm)
- I – luminous intensity (cd)
- π – constant (≈3,14)
- α – apex angle (°)
To calculate luminous intensity (candelas), if luminous flux (lumens) and apex angle (steradians) are known, use this equation:
I=Φ/(2π*(1−cos½*α))
candelas = lumens/(2π*(1-cos½*apex angle))
Now lets check this equation on a more practical example. Lets say we have a lamp that produces 3cd luminous intensity at 40° apex angle and we want to calculate lumens for that lamp. We can use the previous equation:
lm = 3cd*2*π*(1-cos(40°/2))
lm = 18,84*0,06
lm ≈ 1,13 (lighting fixture with 3cd luminous intensity at 40° apex angle would produce luminous flux of approx. 1,13 lumens )
If we increase the viewing angle from 40° to 70° and leave the luminous intensity at 3cd, the total lumen output should increase:
lm ≈ 3,39
So it is true, if we increase the apex angle of a lamp while keeping the luminous intensity the same, the lumen output will also increase.
We can also test this the other way around, lets keep the apex angle at 70°, but reduce the light intensity a half, from 3cd to 1,5cd. Now the lamp should produce less lumens:
lm ≈ 1,69
Which it indeed does, 3,39lm>1,69lm.
Summary of lumens and candelas
To summarise, luminous flux measures the total amount of visible light emitted in all directions, the unit of luminous flux is lumen (lm). Luminous intensity measures the quantity of visible light emitted in a given direction at solid angle by a light source, the unit of luminous intensity is candela (cd). The equation to calculate lumens, when candelas and solid angle of a light source are known is: 1lm = 1cd * sr.
Candelas are mostly used to describe brightness of lighting fixtures that produce focused beam of light at a narrower angle in a single direction, such as laser pointer, flashlight and spot light. Lumens are used to compare bulbs or lighting fixtures that illuminate in a wide angle and need to produce light equally in all directions, such as ceiling lights and some types of food lights. Generally, wider the beam angle of the light, lower the light intensity, and narrower the beam angle of the light, higher the light intensity.
ILLUMINANCE, LUMINANCE, LUX, FOOT-CANDLE
Illuminance
Illuminance is the amount of light or luminous flux falling on a surface. Illuminance is measured in lux (lumens per square meter) or foot-candles (lumens per square foot) using the US and British metrics. Illuminance is independent of type of the surface it illuminates on and only depends on the amount of light that falls on that surface, so it will be the same either when illuminating on a wall, ground, floor, tree or any other object. Illuminance (in opposite to lumens and other lighting metrics) can be easily measured with a simple device called a light meter, or even with a smartphone that has a special application installed.
Lux
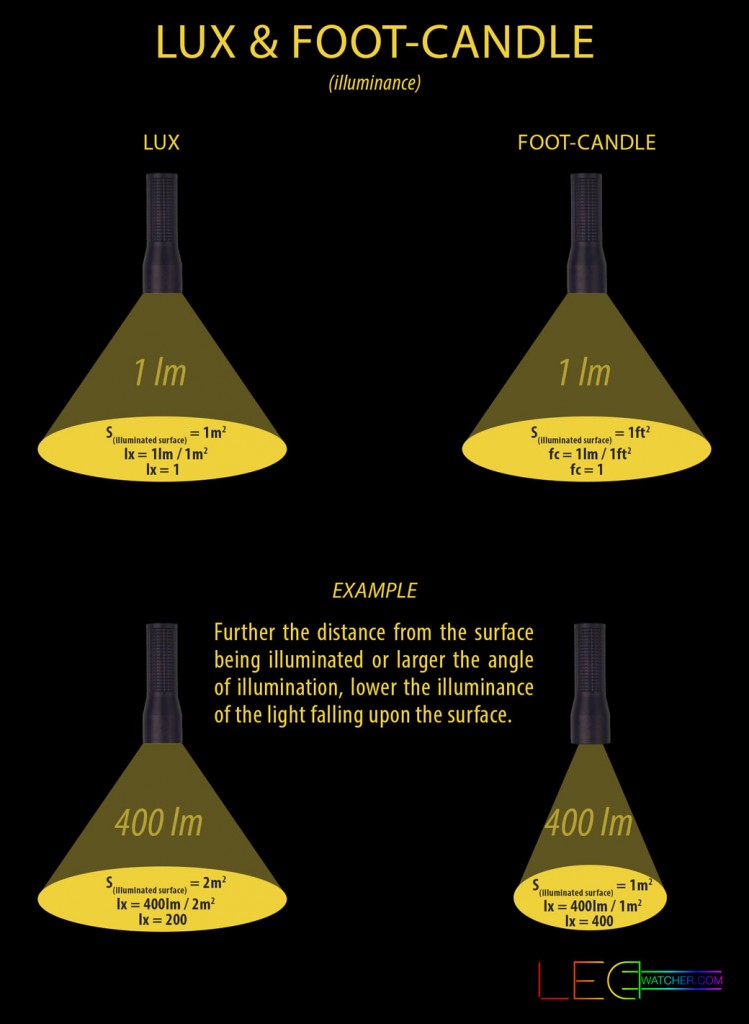
Definition of lux – lux (lx) is a measuring unit of illuminance, lux measures luminous flux per unit area or how much light is falling on a given surface. Basically, lux will determine how bright the surface illuminated is going to be. One lux equals one lumen per square meter of surface area:
1lx = 1lm / m²
or
1lx = 1cd * sr / m²
because 1lm = 1cd * sr
In the above formulas, m² represents the target surface area on which the light is falling on.
Foot-candle
In the Imperial and US customary measurement systems, a term foot-candle (fc) is used instead of lux. Foot-candle also measures the amount of light falling on a surface, but instead of lumens per square meter used to measure lux, lumens per square foot are used to measure foot-candle. One foot-candle equals approx. 10.764 lux. Foot-candles are calculated using the formula:
1fc = 1lm / ft²
Explanation
Illuminance can be easily calculated if luminous flux (lumen) output of a light source and the surface area illuminated are known. For example, a concentrated beam of light with luminous flux of 400 lumens will light up a 1 square meter large area with an illuminance of 400 lux:
lx = 400
However, if we increase the surface area on which the light is falling on two times from 1 square meter to 2 square meters and leave the luminous flux at 400 lumens, the illuminance on that area will decrease two times:
lx = 200
What this means is that the further the distance from the surface being illuminated or larger the angle of illumination, the lower the illuminance of the light falling upon the surface is going to be.
Illuminance is useful when choosing appropriate light bulbs or lighting fixtures for certain areas, such as bedroom, living room, office, shop, theatres, stages and similar areas. Lux is also an important measurement when choosing lighting for growing plants indoors.
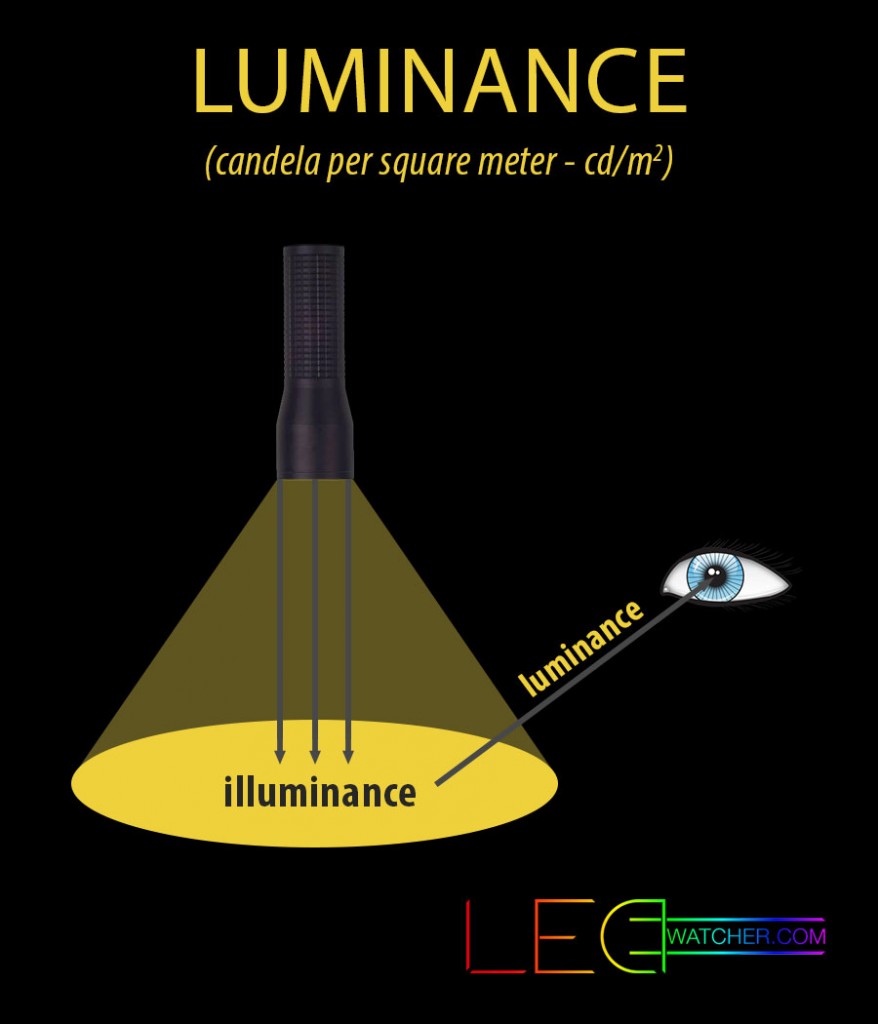
Luminance
Luminance is the luminous intensity that is reflected or emitted from an object per unit area in a specific direction. Luminance depends on how much light is getting to an object and light reflection of that surface. The unit for measuring luminance is candela per square meter – cd/m².
Basically, luminance is used to calculate how much luminous power will be emitted from a given surface at certain viewing angle and detected by a human eye or in other words, how bright will a given surface look to a human eye. Luminance is actually the only light form that we can see. Luminance is used, for example, when making traffic signs and road lighting.
HOW TO MEASURE LIGHT?
Measuring lumens
Many think that lumens for a light bulb or lighting fixture can be easily measured using a cheap light meter or even a mobile app, but in reality it requires a special device called integrating sphere connected to a spectrometer and a computer where special software must be installed that can show multiple metrics such as luminous flux or lumens, luminous efficacy, light spectrum distribution, color temperature and other lighting specifications. So actually, a lumen meter is not a small, portable device you can purchase for couple of bucks but more like a laboratory for measuring lumens and other metrics of light bulbs.
Here is a video from Diode Dynamics showing the integrating sphere used for measuring lumens.
Light meters
There are also other types of meters for measuring different light metrics:
- lux meter for measuring illuminance (lux or foot-candles);
- intensity meter for measuring luminous intensity (candelas);
- luminance meter for measuring luminance.
Lux meters are the most common ones that are used to measure illuminance or the amount of light falling on a surface. Lux light meter is used to measure the amount of light in photography and video filming, in individual houses and many public areas such as offices, shops, libraries, museums and other places to determine if the area has a sufficient level of brightness either for safe working conditions for employees (in offices) or simply for design purposes (in art galleries) and also to determine visibility in outdoor areas, for example, when choosing appropriate street lighting.
Lux meter is often simply called light meter, because of its popularity over other light measuring devices. There are wide range of light meters available on the market based on their price, functionality and precision, starting from couple of dollars up to few hundred dollars for more advanced meters. There are even bunch of lux meter apps (free and paid) available on iOS and Android devices that can measure illuminance and some of these applications are actually pretty decent for basic light measuring tasks.
Light meter apps
Here are few of the most popular light meter apps for iOS or Android devices that you can test out by yourself.
iOS light meter apps:
- Pocket Light Meter (By Nuwaste studios);
- myLightMeter Free (By David Quiles).
Android light meter apps:
- LightMeter Free (By David Quiles);
- Light Meter (Borce Trajkovski);
- beeCam Light Meter (by FM.Bee Corp.).
LUMENS AND WATTAGE
The measurement that describes relation between lumens and watts is luminous efficacy. Luminous efficacy is the ratio between the luminous flux and electric power of a light source, it measures how efficient a light source is at converting electrical power into visible light. The unit of luminous efficacy is lm/W (lumens per watt).
Luminous efficacy calculator
Luminous efficacy can be easily calculated using the equation:
luminous efficacy (lm/W) = luminous flux (lm) / wattage (W)
So, for example, luminous efficacy of a 10 watt light bulb that produces 600 lumens would be 60 lm/W:
600lm / 10W = 60 lm/W
Lumens to watts conversion calculator
We can also transform this equation to calculate wattage of a light bulb if we know luminous flux (lumens) and luminous efficacy of that bulb. Taking the same example, if we know that a light bulb produces 600 lumens with efficacy of 60 lm/W, using equation:
wattage = lumens / lumens per watt hour
600lm / 60lm/W = 10W
we can calculate that that the light bulb will consume 10 watts of electrical power to produce 600 lumens of light.
Watts to lumens conversion calculator
Similarly we can calculate luminous flux (lumens) of a light bulb if we know wattage and luminous efficacy of the bulb, by transforming the same formula:
lumens = wattage * lumens per watt hour
10W * 60 lm/W = 600lm
Lumen comparison
How many lumens are in a watt will depend on the type of bulb used in a lighting fixture. On average, old tungsten incandescent light bulbs will produce 15 lumens per watt while efficient LED bulbs will produce about 75 lumens per watt.
The average lumens to watts conversion for LED, CFL, Halogen and Incandescent light bulbs:
- LED light bulb efficacy ≈ 75 lumens per watt (lm/W);
- CFL light bulb efficacy ≈ 65 lumens per watt (lm/W);
- Halogen light bulb efficacy ≈ 20 lumens per watt (lm/W);
- Incandescent light bulb efficacy ≈ 15 lumens per watt (lm/W).
Lumens chart
Here we have made a lumen comparison chart for LED, CFL, Halogen and Incandescent light bulbs (using the average lumens per watt rating of each type of bulb).







great work
Loved it Arthur! I sell light bulbs at The Home Depot and found your information and knowledge so helpful. Now if a customer has some interesting questions I can run your calculators.
That’s great! Thank you Cathryn.
Your work is fantastic. The best and easiest to understand info available that I have found anywhere. The Calc’s are the easiest and most straight forward available as well. You make these calc’s fun to find the answers. Keep up the GREAT work and THANK YOU VERY MUCH.
I LOVE IT.
Thank you! This keeps me motivated!
Arthur.
This is brilliant.
Thank you